Control charts help analyze data for improving the manufacturing process.

The analysis of data using process behavior charts-Walter Shewhart called them control charts-is the foundation of statistical process control (SPC) for process improvement. SPC focuses on the concept that all processes have routine variation and some processes have additional variation from exceptions. Process improvement requires eliminating causes of exceptional variation, and reducing the variation from routine causes. Correctly constructed, process behavior charts separate exceptional variation from routine variation and allows a user to focus on identifying and removing exceptions from a process.

A variety of process behavior charts have been developed since Shewhart introduced the average and range chart in 1924. One that is widely used, both in manufacturing operations as well as for management processes, is the individuals and moving range chart.

Two charts in one

The individuals and moving range chart-XmR or ImR-are really two charts used in tandem. Together they monitor the process average as well as process variation. Table A summarizes the focus of each chart and gives examples of measures that might be analyzed using this method.

Since the individuals (X) chart is a time-ordered sequence of individual data values, it is possible to see all of the variation, routine and exceptional, from the process on this chart. However, the analysis focuses on separating any exceptional variation present in the data from the routine variation of the process. Quantifying the routine variation is the job of the moving ranges.

How mRs quantify routine variation

Each moving range-absolute difference between adjacent data values-reflects the variation between time periods. The average of the moving ranges is then used to calculate the limits: natural process limits (NPL) on the X chart and upper control limits (UCL) on the mR chart.

If a process has only routine variation, the moving ranges, and thus the average of the moving ranges, can be converted to a standard deviation for the process and used to calculate limits on the charts. These control limits are 3 Sigma limits, as recommended by Shewhart, to ensure the economic control of quality of manufactured product.

If a process has both routine variation and exceptional variation, some moving ranges will be inflated by the exceptions. However, many of the moving ranges will consist only of routine variation, and the average moving range will not be drastically inflated. Limits calculated from the average moving range will still be able to detect exceptional causes of variation. In extreme cases, limits may be calculated from the median moving range. This protects against inflation of the limits on the charts.

Formulas for XmR Chart Limits

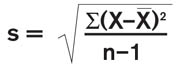
Caution

Two cautions must be recognized. The first temptation is to calculate the control limits for the individual values using all of the data in a traditional formula for standard deviation.

This formula is widely used and is included in many software packages. It is not appropriate to use in calculating limits for the XmR chart because it does not distinguish between routine and exceptional variation. If special cause variation is present in the data, limits calculated using "s" will be overly inflated and no signals will appear on the chart. The ability to detect exceptional variation is undermined by the arithmetic.

The second temptation is to use only the X chart. While this may seem practical, some of the analysis may be lost. The mR chart serves to reinforce the X chart by:

SIDEBAR:

A manufacturer of machined components for the aerospace industry needs to predict productivity for the coming year. Productivity values by shift are available for the past 9 production days and are summarized above.

Using the XmR chart, one individual value and one moving range signal the presence of exceptional variation.

To focus only on routine variation of this process to construct control limits, it is appropriate to calculate the limits using an average moving range, (or median moving range) , without the influence of the data points associated with exceptions. A total of four moving ranges were not used in the final calculation of limits. The final chart clearly distinguishes between routine variation and the additional variation in the data from exceptions. Routine variation in this process is the difference in the NPLs: 99.78-58.65=41.13. Based on this analysis, productivity is not predictable and the variation from routine causes is 41%.