The X, Y and Z axes of the Machine Coordinate System refer to the machine’s motions. When viewed from the front of the machine, the X axis runs from left to right, the Y axis runs from front to back, and the Z axis runs up and down, vertically perpendicular to the other two. Source: Brown & Sharpe

The Part Coordinate System refers to how the three axes—X, Y and Z—refer to datums, or a location. Source: Brown & Sharpe

The coordinate system, invented by the French philosopher and mathematician René Descartes in the early 1600s, is employed in coordinate measuring machines (CMMs) to locate features relative to other features on workpieces.

The coordinate system is like an elevation map where the combination of a letter along one edge of the map, a number along the other and elevations shown throughout uniquely describe each location on the map. This letter/number/elevation combination is called a coordinate and represents a specific place relative to all others.

A CMM's three axes form the machine's coordinate system. The CMM uses a probe to locate points on a workpiece, and each point is unique to the machine's coordinate system. The CMM combines the measured points to form a feature that can be related to all other features.

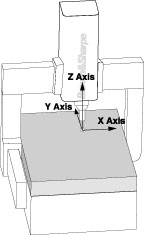
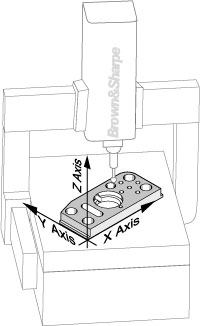
There are two types of coordinate systems used in CMM measurement. The Machine Coordinate System has three axes-X, Y and Z. When viewed from the front of the machine, the X axis runs from left to right, the Y axis runs from front to back, and the Z axis runs up and down, vertically perpendicular to the other two. The second coordinate system is the Part Coordinate System, where the three axes relate to datums. A datum is a location. In metrology, a datum is a feature, such as a hole, surface or slot, on a workpiece.

Before the introduction of computer software to coordinate measurement, parts were physically aligned parallel to the machine's axes so that the Machine and Part Coordinate Systems were parallel to each other. This was time consuming and not very accurate. For round or contoured parts, the measurement task was nearly impossible.

With today's measurement and inspection software, the CMM measures the part's datums (from the part print), establishes the Part Coordinate System and mathematically relates it to the Machine Coordinate System. The process of relating the two coordinate systems is called alignment.

If the inspection requirement is to determine how far a specific feature is from another feature, it is often necessary to translate the origin, or the starting point of the measurement. For example, to find the distance to the centers of each of four holes from a central hole, it is necessary to move the starting point of the measurement to the center of the central hole and then measure the distance to the center of each of the four surrounding holes. The CMM does this automatically when an alignment routine is requested from the software.

Not all datums are at right angles to each other. For example, the distance between two holes not at right angles to each other can be measured when the origin is translated to one hole, and the Part Coordinate System is mathematically rotated so that the holes lie along the newly created axis.

The majority of parts are made up of simple geometric elements created by machining or forming. These primary elements—planes, edges, cylinders, spheres and cones—are called features. When a CMM can measure these features directly with a probe, the features are referred to as measured features. Other features such as distance, symmetry, intersection, angle and projection cannot be measured directly, but must be constructed mathematically from measured features before their values can be determined. These are called constructed features. Source: Brown & Sharpe

Measured and constructed features

The majority of parts are made up of simple geometric elements created by machining or forming. These primary elements-planes, edges, cylinders, spheres and cones-are called features. When a CMM can measure these features directly with a probe, the features are referred to as measured features.

Other features such as distance, symmetry, intersection, angle and projection cannot be measured directly, but must be constructed mathematically from measured features before their values can be determined. These are called constructed features. The relationships between one feature or group of features to another feature or group of features are critical to manufacturing. For example, the intersect point between the cylinders on one side of an engine block and those on the other side determines how well mating parts fit. This intersect point is constructed from the two measured features (the engine cylinders).

A projection is the reproduction of a workpiece feature on another feature, such as projecting a circle or line on a plane, or a point onto a line. Projections facilitate the accurate measurement of how mating parts will fit. Source: Brown & Sharpe

Projections

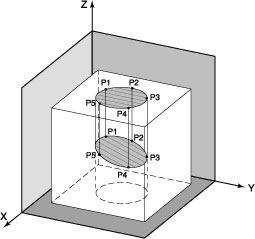
A projection is the reproduction of a workpiece feature on another feature, such as projecting a circle or line on a plane, or a point onto a line. Projections facilitate the accurate measurement of how mating parts will fit. For example, by projecting a cylinder into the plane of the head face during automotive cylinder measurements, it is possible to accurately determine how a piston will fit into the cylinder and how it will meet with the combustion chamber in the head.

A minimum number of three points is necessary to measure the diameter of a circle, and, if those points are not at the same distance from the top of the bore, the measured diameter will be shown to be elliptical. To overcome this misrepresentation, the measurement data is projected onto a plane that is perpendicular to the centerline of the cylinder. The result is an accurate determination of the real size of the feature.