Anyone who has faced a production problem with a need to solve it by using production data can relate to the notion of a brain teaser. The brain teasers presented here are based on real-world situations encountered by workers in manufacturing environments. The brain teasers have three parts: (1) the situation, (2) available data or other supporting information and (3) questions that various workers need answered for continual improvement. Recommended solutions follow in the next issue and on the Web at Quality Online (www.qualitymag.com).

Situation

Arthur works for a company that manufactures specialty lighting for a variety of vehicles. As the senior quality technician, he is responsible for conducting measurement studies on all measurement processes used by his company. One customer requires a report about every six months on the performance of the measurement processes used in the data they receive from Arthur’s company. One such process measures the transmission of light through a special filter used with a specific type of light bulb. All past measurement studies for transmission have passed the customer’s guidelines for a good measurement system. However, the most recent measurement study did not pass all of the guidelines and Arthur is not certain what to do. According to the customer, Arthur should purchase a new transmission device, but he is not so sure.

Available data

Results from the measurement study conducted on March 21, 2006, as well as the results from the recent study on November 9, 2006, are summarized in the table, “Transmission Measurement Study Comparison.” The customer’s guidelines state that the variation from the measurement system multiplied by 6 should not be greater than 40% of the specification range. In the past, Arthur has not seen a problem in meeting this requirement for transmission. Now he sees a problem.

Questions

  1. What is the repeatability of the measurement technique for each of the studies? What is the meaning of repeatability?
  2. What is the reproducibility for each of the studies? How is this number interpreted?
  3. Calculate the percentage of the specification taken by the measurement system variation? Does this meet the customer’s guideline as stated above?
  4. If Arthur believes that his measurement system for transmission is really OK, what specific actions should he take as a result of this measurement study?
    5.


Answers to November Brain Teaser

As the new quality director for a small robot manufacturing company, Melinda is accountable for data provided to customers regarding the critical characteristics of the robots. To meet one customer’s request, she is evaluating software that will create process behavior charts with the data. One package she likes automatically recalculates limits with each data entry. Melinda wants the option to use limits based on a selected set of data, but the software cannot do this.



Q: What is the behavior of the robot arm extension length after the first day?

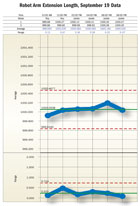
A:The six subgroups of data collected on the first day, September 19, show the robot arm extension length to be predictable at an average of 1,000.0508 millimeters and a standard deviation of 0.1965 millimeter. See the average and range chart, “Robot Arm Extension Length, September 19 Data.”

Q: As each new set of data is used and new limits are calculated, how does the robot arm extension length behave?

A:Using the limits calculated for September 19, the data added on September 20 show the process continues to operate predictably, on the average, for robot arm extension length until noon. The average for the data set at 12:00 p.m. is outside the upper control limit on the average chart. However, if Melinda used the detection rule of 2 points out of 3 beyond a 2-sigma limit, she would have noticed that the range chart shows a detectable increase in variation since the ranges for 8:00 a.m. and 10:00 a.m. are very close to the upper control limit on the range chart. These ranges trigger the detection rule of 2 out of 3 points beyond the 2-sigma limit on a chart. Thus beginning mid-morning on September 20, there are indications that the robot arm extension length has changed. See the chart, “Robot Arm Extension Length, September 19-20.”

Q: What would Melinda have noticed if the limits on the process behavior chart had not been recalculated each time there was new data?

A:If the limits were not recalculated after each new set of data, Melinda would have noticed the changes in the process. The robot arm extension length would be seen as an unpredictable process over the two days.

Q: What are the consequences of continually recalculating limits as new data are collected?

A:As each new set of data is entered in the chart, the recalculated limits would essentially absorb any process changes as they occur. In this case, the new limits get wider and wider while the average increases slowly. By the end of September 20, the average of all the data for both days is 1,000.165 millimeters and the standard deviation is 0.354 millimeter. See the chart, “Robot Arm Extension Length with Control Limits Based on September 19 and 20.”

The standard deviation has been calculated using the formula, , where d2 is a bias correction factor for subgroups of size 2. When the recalculated limits absorb the process changes, those changes often go unnoticed and critical actions required to keep a process running the best it can are not taken in a timely fashion. In fact, it is possible that a process operating in a manner capable of meeting a customer’s specifications could change enough to be incapable without being noticed.