A graded gage block can help achieve a predictable uncertainty without consulting a calibration chart.

When picking up a gage block to check a micrometer or caliper, many operators don't bother to check the gage block's calibration chart because historically gage blocks sold in the United States were extremely accurate. The new B89 gage block tolerances are larger than the old GGG-G-15C tolerances and the new B89 AS1 and AS2 grades may not provide the needed accuracy without consulting a calibration chart. Also, commonly sold "Grade B" sets with tolerances of ±50 microinches are even less accurate. So, operators should know the quality of the gage block when they pick it up to use it.
The purpose of a graded gage block set is to allow operators to choose any block, or combination of blocks, to achieve a predictable uncertainty without having to consult the calibration chart.
Consider a standard 81 or 88 piece Grade 0 gage block set (inch system) that contains blocks from 0.050 to 4 inches in length. A 1-inch block has a tolerance of ±6 microinches.

If viewed graphically, a 1-inch block has a rectangular error distribution where the actual size of the block could be anywhere between -6 and +6 microinches.
Manufacturers sell blocks up to the limits of the tolerances as measured by the manufacturer. Manufacturers also have an uncertainty of measurement. The manufacturer's uncertainty of measurement must be combined with the rectangular error distribution. This combined uncertainty (k=2) is shown in the table "Estimated Uncertainties of Individual Blocks Without Consulting a Calibration Chart" in the columns labeled Error Distribution.

When gage blocks are used in combinations-without using the 2, 3, or 4-inch blocks-the length of a combination of blocks is likely to be between 0.4 and 1.3 inch. A combination to the fourth decimal place is likely to use three blocks below 0.4 inch and one block greater than 0.4 inch.
0.1002
0.107
0.120
0.500
0.8272

For Grade 0 blocks, using the "Estimated Uncertainties of Individual Blocks Without Consulting a Calibration Chart," such a four-block combination would have a combined expanded uncertainty of:

The three "1's" added at the end of the equation are an uncertainty allowance for wringing film thicknesses for three wrings.
If a 1-inch block was added to increase the length of the combination to 1.8272 inch, the combined expanded uncertainty would be:
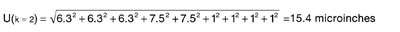
An additional factor of "1" has been added to this equation for an additional wring.

Larger blocks may be added to increase the length of the combination. A table for various grades and approximate sizes of combinations can be made to show the approximate uncertainties of those combinations.
For Grade 0 blocks, a graph showing the uncertainty of combinations vs. the length is nearly linear. The expanded uncertainty (k=2) for combinations of Grade 0 blocks may be approximated by the equation: U = 13 + 1.4L where "L" equals the length of the combination in inches. The same equation can be used for other grades of gage blocks:
Grade 00 U = 8 + 0.667L
Grade 0 U = 13 + 1.4L
Grade AS1 U = 22 + 2.8L
Grade AS2 U = 45 + 5.2L
The maximum length that can comfortably be built with an 81 or 88 piece set is about 12 inches. Then, the maximum uncertainty likely to incur when using a graded set is:
Grade 00 U(max) = 16 µin.
Grade 0 U(max) = 30 µin.
Grade AS1 U(max) = 56 µin.
Grade AS2 U(max) = 108 µin.
To maintain a 4:1 accuracy ratio for calibrations with an accuracy of 0.0001 inch, a Grade 00 set could be used with any combination without consulting the calibration chart. A Grade 0 set could be used with combinations up to 8-inches in length-provided that the sets have been qualified to their grades and all the blocks are in tolerance for that grade. Q
Tech tips
The purpose of a graded gage block set is to allow operators to choose any block, or combination of blocks, to achieve a predictable uncertainty without having to consult the calibration chart.
The manufacturer's uncertainty of measurement must be combined with the rectangular error
distribution.
A table for various grades and approximate sizes of combinations can be made to show the approximate uncertainties of those
combinations.