✕

We make decisions every day based on risk. Some of these decisions are so common that we see them as natural parts of life. Can I see the traffic coming so I can move my car across traffic to safely reach where I am going? Do I need to pack a jacket or umbrella in case of rain later? Many of these decisions are binary (yes or no) and are based on a quick analysis of potential outcomes and their likelihood of positive and negative occurrences for us. With any decision, there is uncertainty in which outcomes and/or occurrence likelihoods are unknown to the decision-maker. How could one know that even though they packed a jacket and umbrella for potential rain, they had not accounted for the bridge to fail and crush them to death? While the likelihood of bridge collapse occurrence was low, the severity of the bridge collapse was high. These potentials are part of the overall uncertainty in life. We have to balance our risk appetite with our desire to live and get things done.

In order for a measurement to be valid, i.e., to have measurement (metrological) traceability, it must be stated with its associated measurement uncertainty. Test or calibration reports with measurement data and its associated uncertainty are information upon which decisions can be made. Is this instrument accurate enough for our use? Can I use this measurement device to calibrate another measurement device? How much product must we scrap to lessen the chance of a failing product being released to the marketplace? How many failing products will we accept in the marketplace? These are all decisions made based on measurements.

In the ISO/IEC 17025 testing and calibration world, there are requirements in ISO/IEC 17025 regarding consideration of measurement uncertainty when making statements of conformity (pass/fail or in-tolerance/out-of-tolerance). This is done using a decision rule. In ISO/IEC 17025:2017, a “decision rule” is defined as a “rule that describes how measurement uncertainty is accounted for when stating conformity with a specified requirement.”¹

The first decision rule requirement is communication of the decision rule and the agreement between the lab and the customer of the decision rule. ISO/IEC 17025:2017, Clause 7.1.3, “When a customer requests a statement of conformity to a specification or standard for the test or calibration (e.g., pass/fail, in-tolerance/out-of-tolerance), the specification or standard and the decision rule shall be clearly defined. Unless inherent in the requested specification or standard, the decision rule selected shall be communicated to, and agreed with, the customer.”²

The second decision rule requirement is ISO/IEC 17025:2017, Clause 7.8.6 Reporting statement of conformity; 7.8.6.1 “When a statement of conformity to a specification or standard is provided, the laboratory shall document the decision rule employed, taking into account the level of risk (such as false accept and false reject and statistical assumptions) associated with the decision rule employed, and apply the decision rule.

NOTE: Where the decision rule is prescribed by the customer, regulations or normative documents, a further consideration of the level of risk is not necessary.

7.8.6.2 The laboratory shall report on the statement of conformity, such that the statement clearly identifies:

a) to which results the statement of conformity applies;

b) which specifications, standards or parts thereof are met or not met;

c) the decision rule applied (unless it is inherent in the requested specification or standard).”³

A common decision rule by many ISO/IEC 17025-accredited calibration labs has been to simply state a decision rule like “Measurement uncertainty is not accounted for when making statements of conformity.” This does not meet the requirement of ISO/IEC 17025, Clause 7.8.6.1 and Accreditation Body assessors are writing findings of deficiencies against this Clause for decision rules stated like that. While measurement uncertainty might not be taken into account when stating a pass or fail, meaning that the pass or fail statement is only based on the measurement value and, not including the measurement uncertainty does NOT mean that the measurement uncertainty’s impact on risk goes away! Just because you are ignoring the elephant in the room does not make the elephant go away!

Let us look at what measurement uncertainty means. In physical measurements, such as in testing and in calibration labs, all measurements have some amount of uncertainty. Measurement uncertainty is defined as a “non-negative parameter characterizing the dispersion of the quantity values being attributed to a measurand, based on the information used.”⁴ To translate into everyday language, it is a non-negative value that is the spread of values around a measured value where the actual values have a defined probability of existing, at the time of the measurement. The spread of the values looks like the normal curve in Figure 1 below.

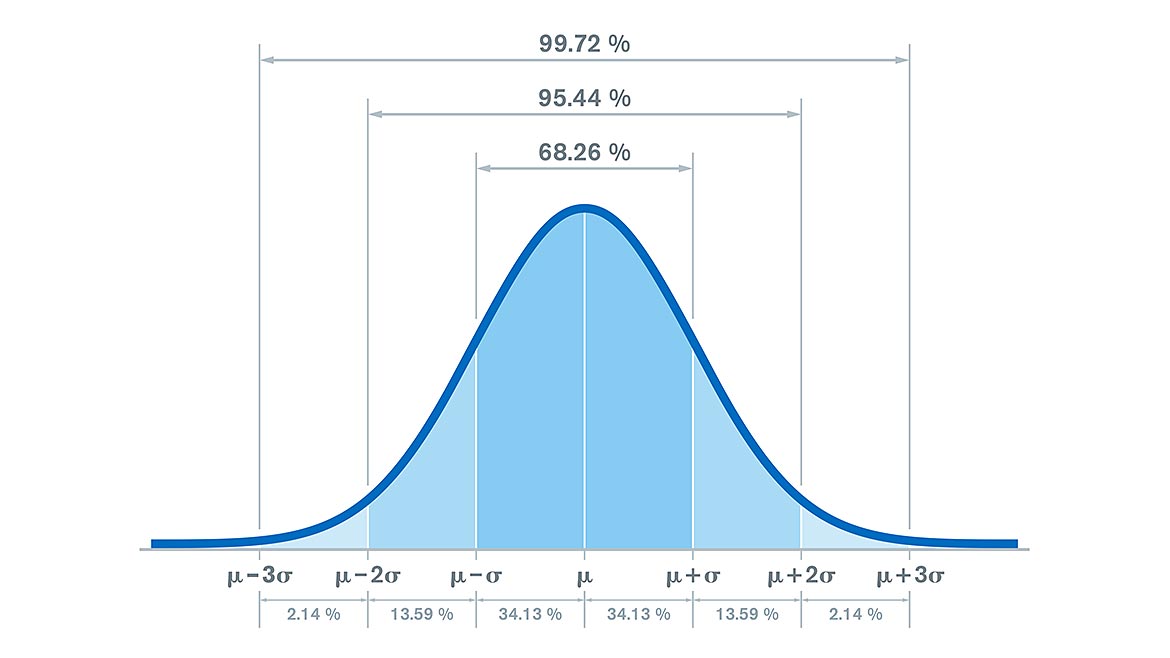
Figure 1. Source: Illustration 209620568 © Peter Hermes Furian | Source: Dreamtime

In Figure 1, the measurement value, µ, is surrounded on both sides by increasing number of standard deviations, σ. Measurement uncertainty reported on test or calibration certificates is reported as an “expanded measurement uncertainty.” Expanded measurement uncertainty is expressed at approximately 95% level of confidence, which usually results in a distribution of 2 standard deviations (2σ). In the figure above, the probability at 2 standard deviations (2σ) is 95.44 %. This means that there is an approximately 95% probability that the measured value exists within 2 standard deviations of the measured value. The number of standard deviations where this 95% probability occurs is identified by the coverage factor, k. We will see how this coverage factor, k, looks like in the statement of uncertainty of measurement.

Now that we have discussed these Greek letters and mind-numbing statistical jargon, let us look at Figure 2 for an example with a measured value, its associated measurement uncertainty, and the specification (tolerance) limits. Our target (nominal) value of 100 units, measured value is also 100 units, a tolerance of 4%, and an expanded measurement uncertainty of 0.98 units (k=2, approximately 95% level of confidence). This means that our measured value is where we expect it, at 100 units. The 4% tolerance means that 4% of our nominal, 100 units, is + 4 units. Our upper specification limit (USL) is 104 units and our lower specification limit (LSL) is 96 units.

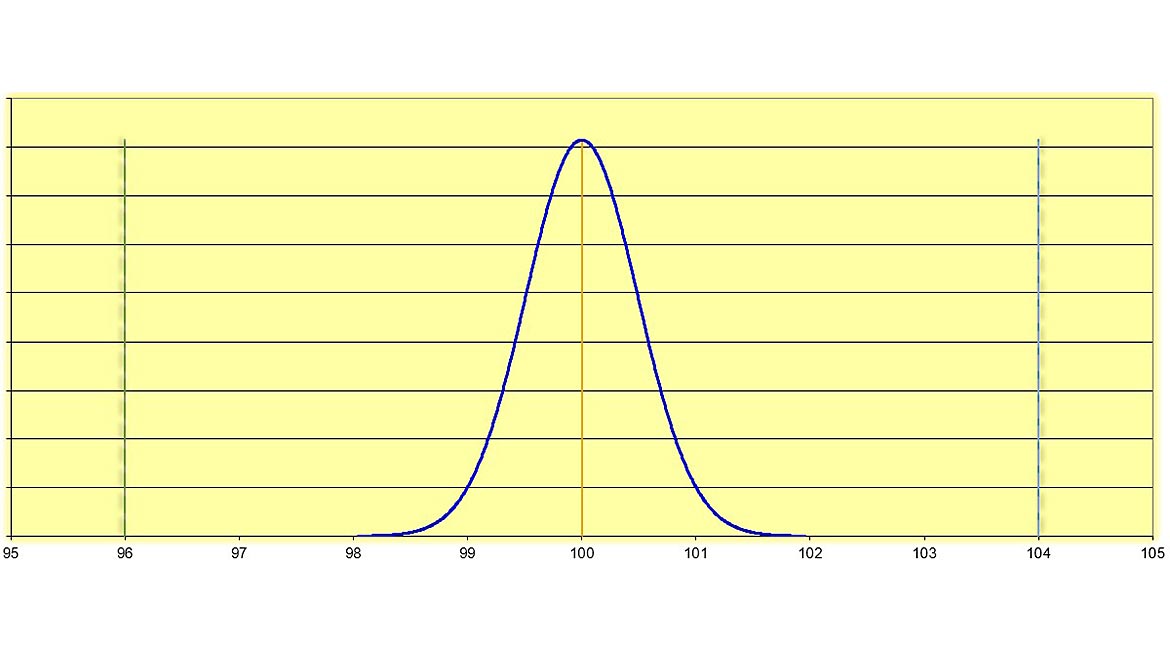
Figure 2 | Source: Dreamtime

In Figure 2, the measured value of 100 units +0.98 units means there is a 95% level of confidence that the measurement is between 99.02 units and 100.98 units. Even when we consider measurement uncertainty in our decision of whether this is in-tolerance or out-of-tolerance when compared to the tolerance limits of 100 units + 4 units, we can confidently say that this measured value is completely in-tolerance.

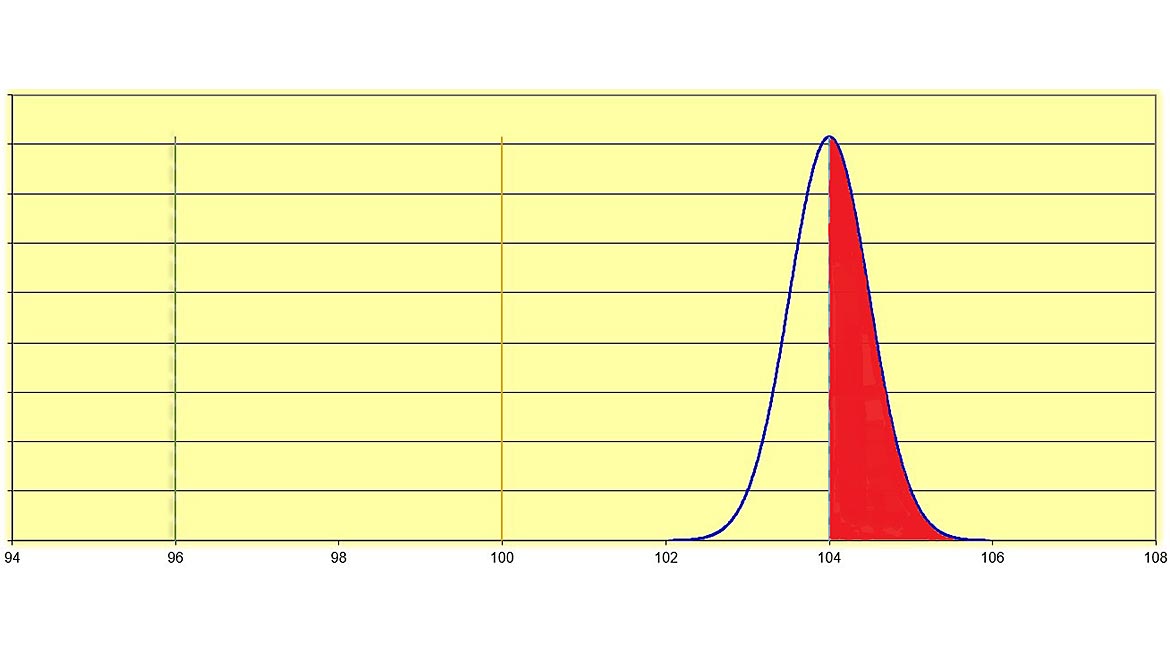
Figure 3 | Source: Dreamtime

Now let us look at an example where the measured value is at the upper specification limit (USL). In Figure 3, the measured value, 104 units, is at the upper specification limit of 104 units. This measurement value has the same measurement uncertainty value as in Figure 2 (+ 0.98 units). The red-shaded part of the normal curve shows the dispersion of values (the measurement uncertainty) that is beyond or outside the tolerance limits, in the out-of-tolerance area. Because the measured value is at the upper specification limit, 50% of the measurement uncertainty is outside the specification limit! While the decision rule may state that measurement values at the specification limit are considered “in-tolerance” and that “measurement uncertainty is not taken into account when making these determinations of in-tolerance or out-of-tolerance,” one can clearly see that there is a 50% risk that the measured value is actually out-of-tolerance. See Figure 4 for the probability of 50% on either side of the measured value at 2 standard deviations in a normal distribution curve.

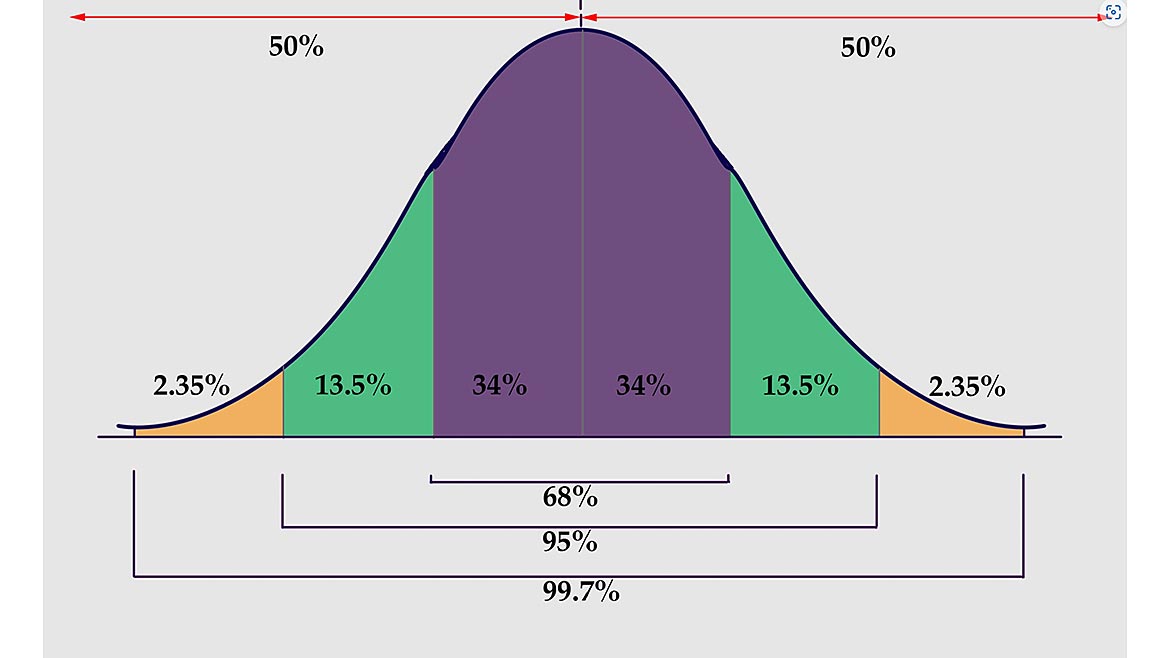
Figure 4 | Source: Dreamtime

We cannot simply ignore the risk associated with a measurement by ignoring its associated uncertainty of measurement. A test report or calibration certificate may include a statement of conformity (pass/fail, in-tolerance/out-of-tolerance) in addition to its reported measurement values. Too many times as customers we simply look for the “Pass” or “Fail” on the certificate and then throw it in a file cabinet. We must look beyond the simple statement of pass or fail and look at where the measured value is and consider the measurement uncertainty to evaluate our risk. By going “Beyond the Sticker and the Cert,” we may be able to prevent some bridges from collapsing.